Propositional Logic Equivalence Laws

In this tutorial we will cover Equivalence Laws.

Equivalence statements

Two statements are said to be equivalent if they have the same truth value.

Example
Following are two statements.
p = It is false that he is a singer or he is a dancer.
q = He is not a singer and he is not a dancer.

The first statement p consists of negation of two simple proposition
a = He is a singer.
b = He is a dancer.
They are connected by an OR operator (connective)
so we can write,
p = ~(a ∨ b)

The second statement q consists of two simple proposition
which are negation of a and b
~a = He is not a singer.
~b = He is not a dancer.
They are connected by an AND operator (connective)
so we can write,
q = ~a ∧ ~b

We have,
p = ~(a ∨ b)
q = ~a ∧ ~b
following are the truth tables for p and q

We can see that the truth values are same for both the statements. So, p and q are equivalent statements.

Now we will cover some equivalence laws.

Properties of 0

If x is a statement then,
0 + x = x
0 . x = 0
where + is the OR operator and
. is the AND operator

Truth table

Properties of 1

If x is a statement then,
1 + x = 1
1 . x = x
where + is the OR operator and
. is the AND operator

Truth table

Involution

If p is a statement then,
~(~p) = p
where ~ is the NOT operator

Truth table

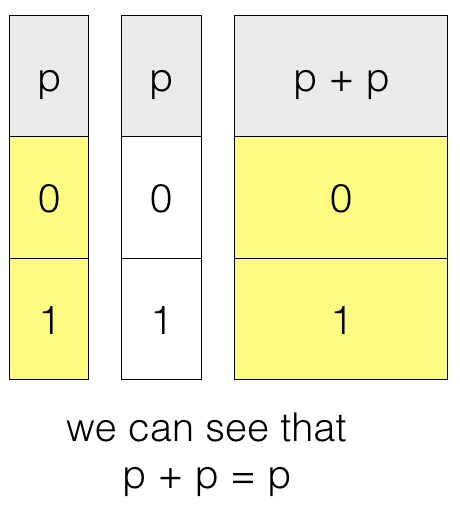
Idempotence Law

If p is a statement then,
p + p = p
p . p = p
where + is the OR operator and
. is the AND operator

Truth table

Absorption Law

If p and q are two statements then,
p + (p.q) = p
p . (p + q) = p
where + is the OR operator and
. is the AND operator

Truth table

Complementarity Law

If p is a statement then,
p + (~p) = 1
p . (~p) = 0
where + is the OR operator,
. is the AND operator and
~ is the NOT operator

Truth table

Commutative Law

If p and q are two statements then,
p + q = q + p
p . q = q . p
where + is the OR operator and
. is the AND operator

Associative Law

If p, q and r are three statements then,
(p + q) + r = p + (q + r)
(p . q) . r = p . (q . r)
where + is the OR operator and
. is the AND operator

Distributive Law

If p, q and r are three statements then,
p . (q + r) = (p . q) + (p . r)
p + (q . r) = (p + q) . (p + r)
p + (~p . q) = p + q
where + is the OR operator,
. is the AND operator and
~ is the NOT operator

De Morgan's Law

If p and q are two statements then,
~(p + q) = ~p . ~q
~(p . q) = ~p + ~q
where + is the OR operator,
. is the AND operator and
~ is the NOT operator

Truth table

Conditional Elimination

If p and q are two statements then,
p ⇒ q = ~p + q
where + is the OR operator and
~ is the NOT operator

Bi-conditional Elimination

If p and q are two statements then,
p ⇔ q = (p . q) + (~p . ~q)
where + is the OR operator,
. is the AND operator and
~ is the NOT operator