Introduction

This is an introduction to Boolean algebra tutorial.

About

Mathematician George Boole invented the Boolean Algebra. This algebra deals with the rules by which logical operations are carried out. So, a digital circuit in this system is represented as input and output symbols and the function of the circuit is expressed as a Boolean relationship between the symbols.

Terms

• Binary Number System
• Binary Constant
• Binary Variable
• Basic Logical Operation
• Boolean Function

Binary Number System

It is a number system consisting of only two digits 0 and 1. It is also called the base 2 number system. All the numbers in this system is expressed in 0s and 1s.

Example: Decimal number (8)10 is written as (1000)2 in binary.

Binary Constant

A binary value that will not change is called a binary constant.

Binary Variable

A binary variable is a symbolic name assigned to a binary value.

Example: A = 1010

Here, A is a variable having binary value 1010.

Basic Logical Operation

Following are the basic logical operation.

• OR operation (+)
• AND operation (.)
• NOT operation (')

The Logical OR operation (+)

Logical OR operation of two boolean variables A and B is written as X = A + B

It is also called logical addition.

The following table contains the input and output of the logical OR operation.

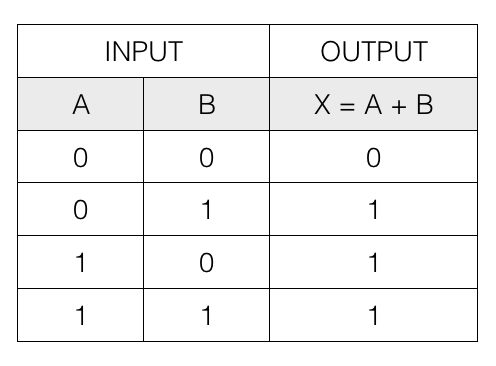
So, if any one of the input is 1 then the output is 1, otherwise it is 0.

The Logical AND operation (.)

Logical AND operation of two boolean variables A and B is written as X = A . B

It is also called logical multiplication.

The following table contains the input and output of the logical AND operation.

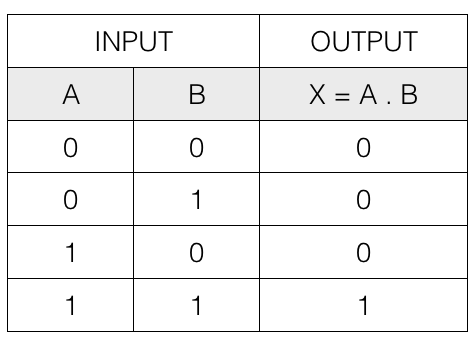
So, if both the input is 1 then the output is 1, otherwise it is 0.

The Logical NOT operation (')

Logical NOT operation performs inverse operation and converts 1 into 0
and 0 into 1.

The following table contains the input and output of the logical NOT operation.

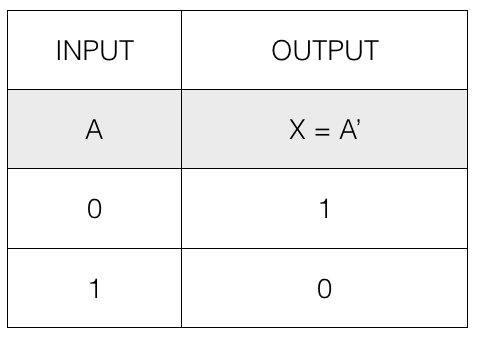
So, if the input is 1 then the output is 0 and if the input is 0 then the output is 1.

Boolean Function

A boolean function is an algebraic expression formed using binary constants, binary variables and basic logical operators.

Example: Boolean Function
F = A + 1

where, A is a binary variable
+ is a Basic Logical Operator (OR)
and, 1 is a binary constant.