Product of Sums reduction using Karnaugh Map - Boolean Algebra - dyclassroom

In this tutorial we will learn to reduce Product of Sums (POS) using Karnaugh Map.

Reduction rules for POS using K-map

There are a couple of rules that we use to reduce POS using K-map. First we will cover the rules step by step then we will solve problem. So lets start...

Pair reduction Rule

Consider the following 4 variables K-map.

Now we mark the cells in pair (set of 2) having value 0.

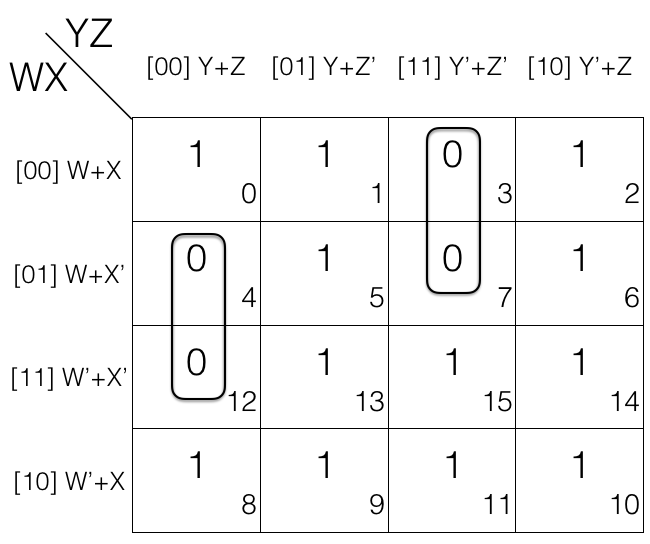
1st pair = (W+X’+Y+Z) . (W’+X’+Y+Z)
2nd pair = (W+X+Y’+Z’) . (W+X’+Y’+Z’)
(the pairs are in Product of Sums POS form)

Now we will remove the variable that changed in the 1st and 2nd pair. Looking at the 1st pair W changed to W’ so we remove it. Looking at the 2nd pair X changed to X’ so we remove it.

So the updated pairs after reduction are given below.

1st pair
= (W+X’+Y+Z) . (W’+X’+Y+Z)
= (X’+Y+Z)

2nd pair
= (W+X+Y’+Z’) . (W+X’+Y’+Z’)
= (W+Y’+Z’)

Note! pair reduction rule removes 1 variable.

Quad reduction Rule

Consider the following 4 variables K-map.

Mark the cells in quad (set of 4) having value 0.

1st quad = (W+X+Y+Z) . (W+X’+Y+Z) . (W’+X’+Y+Z) . (W’+X+Y+Z)
2nd quad = (W+X+Y’+Z’) . (W+X+Y’+Z) . (W+X’+Y’+Z’) . (W+X’+Y’+Z)
(the quads are in Product of Sums POS form)

Now we will remove the variable that changed in the 1st and 2nd quad. Looking at the 1st quad W’ and X’ changed to W and X so, we remove them and looking at the 2nd quad X’ and Z changed to X and Z’ so, we remove them.

So the updated quads after reduction

1st quad
= [(W+X+Y+Z) . (W+X’+Y+Z)] . [(W’+X’+Y+Z) . (W’+X+Y+Z)]
= (W+Y+Z) . (W’+Y+Z)
= (Y+Z)

2nd quad
= [(W+X+Y’+Z’) . (W+X+Y’+Z)] . [(W+X’+Y’+Z’) . (W+X’+Y’+Z)]
= (W+X+Y’) . (W+X’+Y’)
= (W+Y’)

Note! quad reduction rule removes 2 variables.

Octet reduction Rule

Consider the following 4 variables K-map.

Mark the cells in octet (set of 8) having value 0.

octet
= (W+X+Y+Z) . (W+X+Y+Z’) . (W+X+Y’+Z’) . (W+X+Y’+Z)
. (W+X’+Y+Z) . (W+X’+Y+Z’) . (W+X’+Y’+Z’) . (W+X’+Y’+Z)

(the octet is in Product of Sums POS form)

Now we will remove the variable that changed in the octet. Looking at the octet moving top to bottom: X’ changed to X, moving from left to right: Y’ changed to Y and moving from left to right: Z’ changed to Z.

Updated octet after reduction

octet
= [(W+X+Y+Z) . (W+X+Y+Z’)]
. [(W+X+Y’+Z’) . (W+X+Y’+Z)]
. [(W+X’+Y+Z) . (W+X’+Y+Z’)]
. [(W+X’+Y’+Z’) . (W+X’+Y’+Z)]

= [(W+X+Y) . (W+X+Y’)]
. [(W+X’+Y) . (W+X’+Y’)]

= (W+X) . (W+X’)
= W

Note! octet reduction rule will remove 3 variables.

Map Rolling reduction Rule

In this we consider that the K-map top edge is connected with the bottom edge and left edge is connected with the right edge then we mark the pairs, quads and octets. Lets check few examples.

Map Rolling reduction Rule - marking the pairs

Consider the following 4 variables K-map.

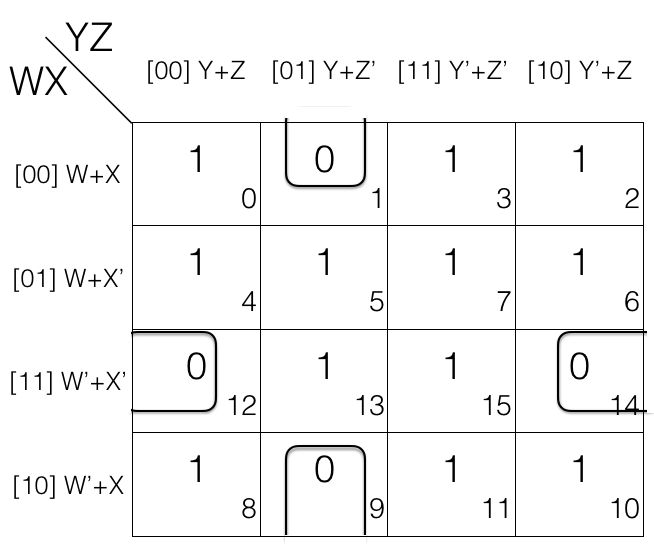
1st pair = (W+X+Y+Z’) . (W’+X+Y+Z’)

2nd pair = (W’+X’+Y+Z) . (W’+X’+Y’+Z)

in 1st pair W change to W’
in 2nd pair Y change to Y’

so we will remove them.

Updated pairs after reduction

1st pair
= (W+X+Y+Z’) . (W’+X+Y+Z’)
= (X+Y+Z’)

2nd pair
= (W’+X’+Y+Z) . (W’+X’+Y’+Z)
= (W’+X’+Z)

Map Rolling reduction Rule - marking the quads

Consider the following 4 variables K-map.

1st quad
= (W+X+Y+Z’) . (W+X+Y’+Z’) . (W’+X+Y+Z’) . (W’+X+Y’+Z’)

2nd quad
= (W+X’+Y+Z) . (W’+X’+Y+Z) . (W+X’+Y’+Z) . (W’+X’+Y’+Z)

In 1st quad and 2nd quad W’ change to W and Y’ changes to Y so we will remove them.

Updated quads after reduction

1st quad
= [(W+X+Y+Z’) . (W+X+Y’+Z’)] . [(W’+X+Y+Z’) . (W’+X+Y’+Z’)]
= (W+X+Z’) . (W’+X+Z’)
= (X+Z’)

2nd quad
= [(W+X’+Y+Z) . (W’+X’+Y+Z)] . [(W+X’+Y’+Z) . (W’+X’+Y’+Z)]
= (X’+Y+Z) . (X’+Y’+Z)
= (X+Z)

Map Rolling reduction Rule - marking the octets

Consider the following 4 variables K-map.

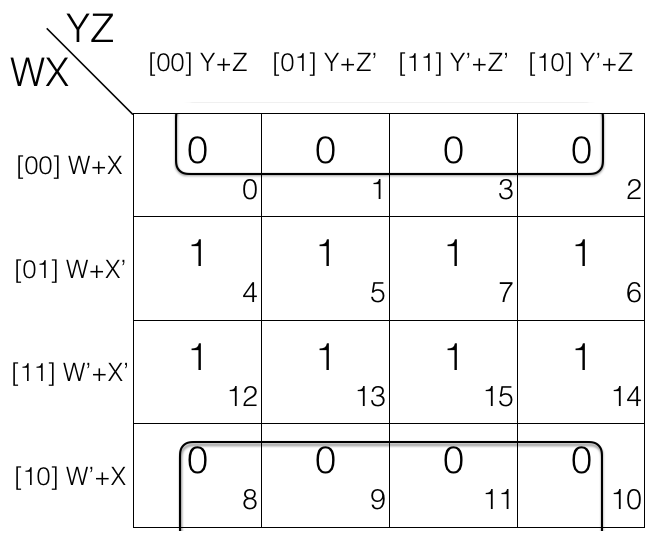
octet
= (W+X+Y+Z) . (W+X+Y+Z’)
. (W+X+Y’+Z’) . (W+X+Y’+Z)
. (W’+X+Y+Z) . (W’+X+Y+Z’)
. (W’+X+Y’+Z’) . (W’+X+Y’+Z)

Looking at the octet we can tell that W’ changed to W, Y’ changed to Y and Z’ changed to Z so we will remove them.

octet
= [(W+X+Y+Z) . (W+X+Y+Z’)]
. [(W+X+Y’+Z’) . (W+X+Y’+Z)]
. [(W’+X+Y+Z) . (W’+X+Y+Z’)]
. [(W’+X+Y’+Z’) . (W’+X+Y’+Z)]

= [(W+X+Y) . (W+X+Y’)]
. [(W’+X+Y) . (W’+X+Y’)]
= (W+X) . (W’+X)
= X

Overlapping Groups

When a value in a cell of K-map is encircled in more that one group (pair, quad or octet) then we call such groups an overlapping groups. Lets check an example...

Overlapping Groups - marking the overlapping groups

Consider the following 4 variables K-map.

1st pair = (W+X’+Y+Z) . (W+X’+Y+Z’)
= M₄ . M₅

2nd pair = (W’+X’+Y’+Z’) . (W’+X’+Y’+Z)
= M₁₅ . M₁₄

quad = [(W+X’+Y+Z’) . (W+X’+Y’+Z’)]
. [(W’+X’+Y+Z’) . (W’+X’+Y’+Z’)]
= M₅ . M₇ . M₁₃ . M₁₅

If we look at M₅ and M₁₅ they are overlapping.

Overlapping groups helps in getting simpler expression after reduction.

1st pair = (W+X’+Y+Z) . (W+X’+Y+Z’)
= (W+X’+Y)

2nd pair = (W’+X’+Y’+Z’) . (W’+X’+Y’+Z)
= (W’+X’+Y’)

quad = [(W+X’+Y+Z’) . (W+X’+Y’+Z’)]
. [(W’+X’+Y+Z’) . (W’+X’+Y’+Z’)]
= (W+X’+Z’) . (W’+X’+Z’)
= X’+Z’

Redundant Groups

After marking out the overlapping groups it is important to also check for redundant groups. If all the values of a group G (pair, quad or octet) is covered (overlapping) with other groups then that group G is redundant and ignored. Lets check an example.

Finding the redundant groups

Consider the following 4 variables K-map.

1st pair = M₅ . M₇

2nd pair = M₁₂ . M₁₃

3rd pair = M₅ . M₁₃

If we look at M₅ and M₁₃ i.e. 3rd pair, it is a redundant group as M₅ and M₁₃ is covered in 1st and 2nd pair so we will remove the redundant group (3rd pair).

Updated pairs after reduction

1st pair = M₅ . M₇
= (W+X’+Y+Z’) . (W+X’+Y’+Z’)
= (W+X’+Z’)

2nd pair = M₁₂ . M₁₃
= (W’+X’+Y+Z) . (W’+X’+Y+Z’)
= (W’+X’+Y)

Summary of Reduction rules for POS using K-map

Prepare the truth table for the function
Draw an empty K-map (2-variables, 3-variables, so on)
Fill the cells with value 0 for which the output is 0
Fill rest of the cells with value 1
Mark the Octets, Quads and Pairs by encircling the value 0s (also check map rolling, overlapping groups and remove redundant groups)
AND (.) the reduced expression to get the final answer

Time to solve problem :-)

POS reduction using K-map

Reduce F(A,B,C,D) = ∏(0,1,2,4,5,7,10,15) using K-map. Since function F has 4 variables so we will create a 4 variable K-map having 2⁴ = 16 cells.

Now fill the cell marked with subscript 0,1,2,4,5,7,10 and 15 with value 0 as we are dealing with Product of Sums POS. And fill rest of the cells with value 1.

Now we will mark the octets, quads and pairs.

Looking at the K-map we can tell that there is no octets so we will look for quads.

Looking for quads and marking them.

No more quad left so we will now look for pairs and mark them.

No more pairs left so we will move to map rolling and look for octet, quad and pair.

There is no octet and quad but on map rolling we do find a pair. So marking the pair.

Now looking for overlapping groups.

If we look at the K-map we will see that M₇ in pair (M₅,M₇) and pair (M₇, M₁₅) is shared in both the groups so both the pairs are overlapping groups.

Similarly M₅ in pair (M₅,M₇) and quad (M₀, M₁, M₄, M₅) is shared in both the groups so the pair and quad are overlapping groups.

And there is no other overlapping groups so we will now check for redundant groups.

Check for redundant groups.

Looking at the K-map we can tell pair (M₅,M₇) is redundant as M₅ is covered in quad (M₀, M₁, M₄, M₅) and M₇ is covered in pair (M₇, M₁₅) so we will remove the pair (M₅,M₇).

Now we will write down the marked groups and find the reduced expression.

quad = M₀ . M₁ . M₄ . M₅
= [(W+X+Y+Z) . (W+X+Y+Z’)]
. [(W+X’+Y+Z) . (W+X’+Y+Z’)]
= (W+X+Y) . (W+X’+Y)      [Z’ changed, so removed]
= (W+Y)      [X’ changed, so removed]

1st pair = M₇ . M₁₅
= [(W+X’+Y’+Z’) . (W’+X’+Y’+Z’)]
= (X’+Y’+Z’)      [W’ changed to W, so removed]

2nd pair = M₂ . M₁₀
= [(W+X+Y’+Z) . (W’+X+Y’+Z)]
= (X+Y’+Z)      [W’ changed to W, so removed]

Now we AND (.) the results to get the final reduced expression.

F = (W+Y) . (X’+Y’+Z’) . (X+Y’+Z)

This is the required answer.