Kruskal Algorithm - Finding Minimum Spanning Tree

In this tutorial we will learn to find Minimum Spanning Tree (MST) using Kruskal's Algorithm.

Graph

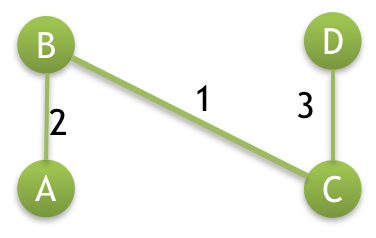
Consider the following graph.

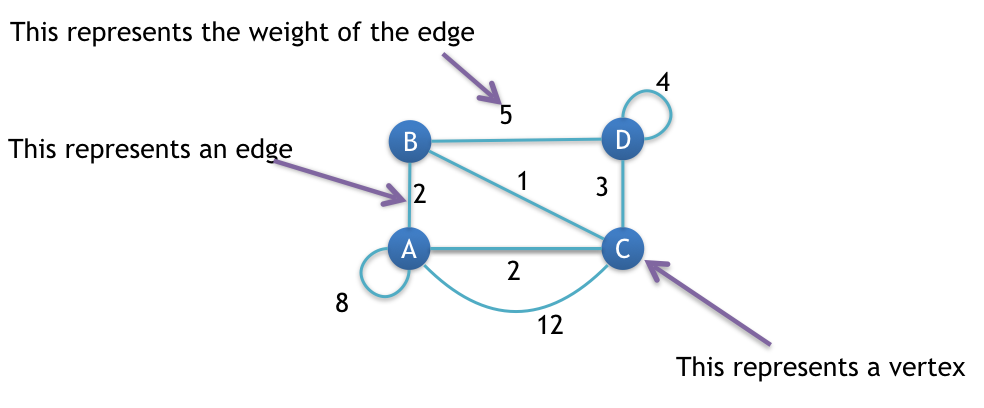
We will find MST for the above graph shown in the image.

Steps

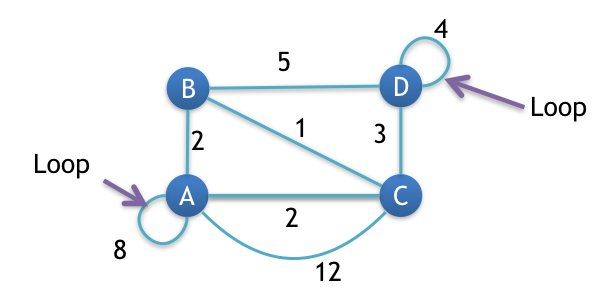
Step 1: Remove all loops

Any edge that starts and ends at the same vertex is a loop.

Loops are marked in the image given below.

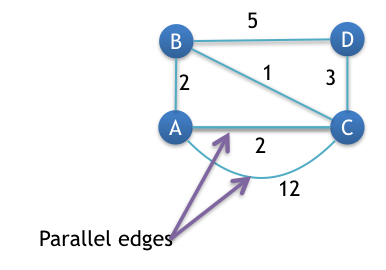
Step 2: Remove all parallel edges between two vertex except the one with least weight

In this graph, vertex A and C are connected by two parallel edges having weight 2 and 12 respectively. So, we will remove 12 and keep 2.

We are now ready to find the MST – Minimum Spanning Tree.

Step 3: Create the edge table

An edge table will have name of all the edges along with their weight is ascending order.

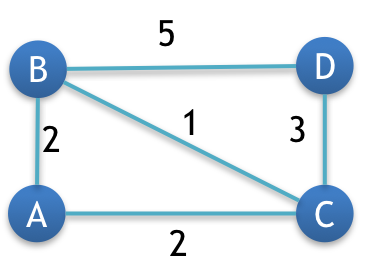
Now if you look at the graph, then you will notice that there are total 5 edges. So our edge table will have 5 columns.

Note! Our graph has 4 vertices so, our MST will have 3 edges.

How we will proceed

To find the MST (Minimum Spanning Tree) we will start from the smallest weight edge and keep selecting edges that does not form any circuit with the previously selected edges.

Result

Pseudo Code

/**
 * G = input graph
 * MST = Minimum Spanning Tree graph
 * E = no. of Edges
 * V = no. of Vertices
 *
 * Assumed that G has no loop and no parallel edges
 */

Given: G(E,V)

// sort edges in ascending order by weight
sort(G)

// create MST
Create: MST(V-1, V)  // total edges of MST = V-1, total vertices = V

// find MST
set: j = 0;
set: i = 0;

while (i < E and j < V-1) do
  
  // temporarily add edge[i] of graph G to graph MST
  set: MST->edge[j] = G->edge[i];
  set: MST->E = j + 1;

  // check if graph MST has no cycle after adding the edge[i] of graph G
  if !hasCycle(MST) then

    // we are keeping the edge[i] of G in MST
    set: j = j + 1;

  endif

  set: i = i + 1;

endwhile

display: MST

Code

Note! In the given code we are representing Vertices using decimal numbers.
So,
vertex A is denoted by digit 0.
vertex B is denoted by digit 1.
vertex C is denoted by digit 2.
vertex D is denoted by digit 3.

/**
 * file: kruskal.c
 * author: yusuf shakeel
 * date: 2014-03-01
 *
 * description: find the MST using kruskal algorithm.
 *
 * vertices are numbered from 0.
 * so,
 * vertex A becomes 0
 * vertex B becomes 1
 * and so on...
 */

#include <stdio.h>
#include <stdlib.h>

/**
 * weighted edge of the graph
 */
struct Edge {

  int start;    //starting vertex (node) of the edge
  int end;    //ending vertex (node) of the edge
  int weight;    //weight of the edge

};

/**
 * the graph
 */
struct Graph {

  int E;    //number of edges in the graph
  int V;    //number of vertices in the graph
  struct Edge* edge;  //pointer to array of edges
  
};

/**
 * this is for the subset
 */
struct subset {
  
  int parent;    //this is the parent of the subset
  int rank;    //this is the rank of the subset

};

/**
 * this function will create a graph and will return pointer to the graph
 */
struct Graph* createGraph(int E, int V) {

  //creating graph pointer
  struct Graph* graph = (struct Graph*) malloc (sizeof(struct Graph));
  
  //assign no. of edge and no. of vertex
  graph->E = E;
  graph->V = V;

  //pointer to edge
  graph->edge = (struct Edge*) malloc (graph->E * sizeof(struct Edge));

  //return graph pointer
  return graph;

}

/**
 * this function will find the subset in which
 * the vertex i belongs
 */
int Find(struct subset subsets[], int i) {
  
  if (subsets[i].parent != i) {

    subsets[i].parent = Find(subsets, subsets[i].parent);

  }
  
  return subsets[i].parent;

}

/**
 * this function will perform union operation on two subsets
 */
void Union(struct subset subsets[], int vertXSubset, int vertYSubset) {

  int rootOfX = Find(subsets, vertXSubset);
    int rootOfY = Find(subsets, vertYSubset);
 
    if (subsets[rootOfX].rank < subsets[rootOfY].rank) {
     
        subsets[rootOfX].parent = rootOfY;

    }
    else if (subsets[rootOfX].rank > subsets[rootOfY].rank) {

        subsets[rootOfY].parent = rootOfX;

    }
    else {

        subsets[rootOfY].parent = rootOfX;
        subsets[rootOfX].rank++;

    }
}

/**
 * this function will sort the edges of a graph by weight
 * in ascending order
 */
void sort(struct Graph* graph) {

  //variables
  int i, j, noOfEdges = graph->E;
  struct Edge* tempEdge = (struct Edge*) malloc (sizeof(struct Edge));

  //bubble sort
  //you can use any other sorting of your choice
  for (i = 1; i < noOfEdges; i++) {
    for (j = 0; j < noOfEdges - i; j++) {

      if (graph->edge[j].weight > graph->edge[j+1].weight) {

        tempEdge->start = graph->edge[j].start;
        tempEdge->end = graph->edge[j].end;
        tempEdge->weight = graph->edge[j].weight;

        graph->edge[j] = graph->edge[j+1];

        graph->edge[j+1].start = tempEdge->start;
        graph->edge[j+1].end = tempEdge->end;
        graph->edge[j+1].weight = tempEdge->weight;

      }
    }
  }

}

/**
 * this function will display the MST (minimum spanning tree)
 */
void displayMST(struct Graph* graphMST) {
  int i, noOfEdges = graphMST->E;
  for (i = 0; i < noOfEdges; i++) {
    printf("Edge %d-->%d Weight: %d\n", graphMST->edge[i].start, graphMST->edge[i].end, graphMST->edge[i].weight);
  }
}

/**
 * this function will return 1 if cycle is found
 * in the graph otherwise 0
 */
int hasCycle(struct Graph* graph) {

  //variable
  int i, j, vertXSubset, vertYSubset;

  //total number of vertices in the graph
  int V = graph->V;
  int E = graph->E;

  /**
   * create subset
   */
  struct subset* subsets = (struct subset*) malloc (V * sizeof(struct subset));

  //initialize subset
  for (i = 0; i < V; i++) {

    subsets[i].parent = i;
    subsets[i].rank = 0;

  }

  //detect cycle
  for (j = 0; j < E; j++) {

    vertXSubset = Find(subsets, graph->edge[j].start);
    vertYSubset = Find(subsets, graph->edge[j].end);

    if (vertXSubset == vertYSubset) {

      return 1;

    }

    Union(subsets, vertXSubset, vertYSubset);

  }
  

  return 0;

}

/**
 * kruskal function to compute MST
 */
void kruskal(struct Graph* graph) {

  //variables
  int i, j;

  //number of edges and vertices in the graph
  int E = graph->E;
  int V = graph->V;

  /**
   * sort the edges of the graph in ascending order of weight
   */
  sort(graph);
  
  /**
   * MST graph
   */
  struct Graph* graphMST = createGraph(V - 1, V);

  /**
   * find MST
   */
  //now check other edges
  for (i = 0, j = 0; i < E && j < V - 1; i++) {

    graphMST->edge[j] = graph->edge[i];
    graphMST->E = j + 1;

    if (!hasCycle(graphMST)) {

      j++;

    }

  }


  /**
   * display the computed MST (minimum spanning tree)
   */
  displayMST(graphMST);

}

/**
 * the main function
 */
int main (void) {

  //total number of edges and vertices
  int E = 5;
  int V = 4;

  /**
   * create graph
   */
  struct Graph* graph = createGraph(E, V);

  /**
   * add edges to the graph
   */
  //edge: A -- B
  graph->edge[0].start = 0;
  graph->edge[0].end = 1;
  graph->edge[0].weight = 2;
  
  //edge: A -- C
  graph->edge[1].start = 0;
  graph->edge[1].end = 2;
  graph->edge[1].weight = 2;
  
  //edge: B -- C
  graph->edge[2].start = 1;
  graph->edge[2].end = 2;
  graph->edge[2].weight = 1;
  
  //edge: B -- D
  graph->edge[3].start = 1;
  graph->edge[3].end = 3;
  graph->edge[3].weight = 5;
  
  //edge: D -- C
  graph->edge[4].start = 3;
  graph->edge[4].end = 2;
  graph->edge[4].weight = 3;

  /**
   * find MST using kruskal
   */
  kruskal(graph);

  return 0;
}

Output

Edge 1-->2 Weight: 1
Edge 0-->1 Weight: 2
Edge 3-->2 Weight: 3