Longest Common Subsequence

In this tutorial we will learn to find the Longest Common Subsequence for a given sequence using Dynamic Programming.

About Longest Common Subsequence or LCS

Given two sequence say "ABCD" and "ACF".

Longest Common Subsequence or LCS is a sequence that appears in the same relative order in both the given sequences but not necessarily in a continuous manner.

LCS for the given sequences is AC and length of the LCS is 2.

Another Example

Given two sequence say "ABACCD" and "ACDF"

Find Longest Common Subsequence or LCS

Given two sequences:

ABACCD      ACDF
^           ^
SAME (so we mark them and move to next letters)


[A]BACCD    [A]CDF
   ^           ^
DIFFERENT (so move to next letter)


[A]BACCD    [A]CDF
    ^          ^
DIFFERENT (so move to next letter)


[A]BACCD    [A]CDF
     ^         ^
SAME (so we mark them and move to next letters)


[A]BA[C]CD  [A][C]DF
        ^         ^
DIFFERENT (so move to next letter)


[A]BA[C]CD  [A][C]DF
         ^        ^
SAME (so we mark them)


[A]BA[C]C[D]    [A][C][D]F

So, LCS for the given sequences is ACD and length of the LCS is 3.

Solving LCS problem using Dynamic Programming

Consider following two sequences.

Length (number of characters) of sequence X is XLen = 4

And length of sequence Y is YLen = 3

Create Length array

Now create a Length array L. It will contain the length of the required longest common subsequence. L is a two dimensional array.

Having rows = XLen + 1 = 4+1 = 5

And columns = YLen + 1 = 3+1 = 4

Fill the row 0 with 0 and col 0 with 0.

Rule to fill the Length array L


if (X[r-1] == Y[c-1]) then
  L[r][c] = L[r-1][c-1] + 1
else
  L[r][c] = max { L[r-1][c], L[r][c-1] }

i.e., if current character in X and Y are same
then they are in the resulting LCS.

After filling up the L array it will look as follows.

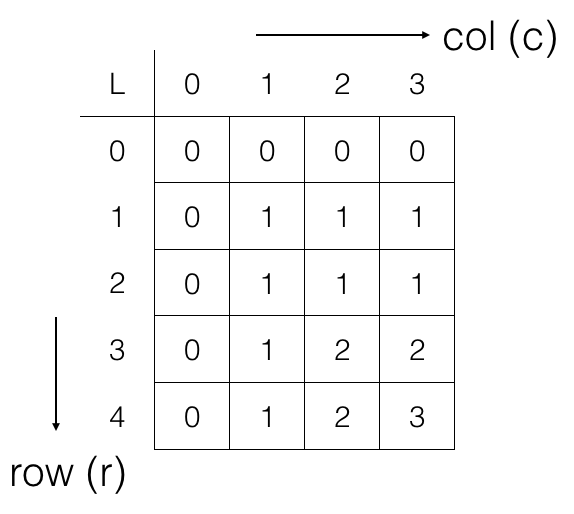
The length of the Longest Common Subsequence LCS

To know the length of the longest common subsequence for X and Y we have to look at the value L[XLen][YLen],
i.e., L[4][3] = 3

So, Length of LCS = L[4][3] = 3

Find the LCS

Create an array LCS of size 3, this will hold the characters in the LCS for the given two sequences X and Y.

Rule to fill the LCS array


Set r = XLen, c = YLen, i = L[r][c]
while ( r > 0 && c > 0) do
  if (X[r-1] == Y[c-1]) then
    LCS[i-1] = X[r-1]
    i = i - 1,  r = r - 1,  c = c - 1
  else if (L[r-1][c] > L[r][c-1]) then
    r = r - 1
  else
    c = c - 1
endwhile

After filling up the LCS array it will look like the following.

Required Longest Common Subsequence [LCS] is ACF.

Code in C


#include<stdio.h>
#include<string.h>

int max(int a, int b);
void findLCS(char *X, char *Y, int XLen, int YLen);

int max(int a, int b) {
  return (a > b)? a : b;
}

void findLCS(char *X, char *Y, int XLen, int YLen) {
  int L[XLen + 1][YLen + 1];
  int r, c, i;

  /*
   * find the length of the LCS
   */
  for(r = 0; r <= XLen; r++) {

    for(c = 0; c <= YLen; c++) {

      if(r == 0 || c == 0) {

        L[r][c] = 0;

      } else if(X[r - 1] == Y[c - 1]) {

        L[r][c] = L[r - 1][c - 1] + 1;

      } else {

        L[r][c] = max(L[r - 1][c], L[r][c - 1]);
      }
    }
  }

  /*
   * Print LCS
   */
  r = XLen;
  c = YLen;
  i = L[r][c];

  char LCS[i+1];

  /*
   * setting the NULL character at the end of LCS character array.
   * as we know in C programming language, NULL character is used
   * to denote the end of a string
   */
  LCS[i] = '\0';

  while(r > 0 && c > 0) {

    if(X[r - 1] == Y[c - 1]) {

      LCS[i - 1] = X[r - 1];

      i--;
      r--;
      c--;

    } else if(L[r - 1][c] > L[r][c - 1]) {

      r--;

    } else {

      c--;

    }

  }

  //print result
  printf("Length of the LCS: %d\n", L[XLen][YLen]);
  printf("LCS: %s\n", LCS);
}

int main(void) {
  //the two sequences
  char X[] = "ABCF";
  char Y[] = "ACF";

  //length of the sequences
  int XLen = strlen(X);
  int YLen = strlen(Y);

  findLCS(X, Y, XLen, YLen);

  return 0;
}

Output

Length of the LCS: 3
LCS: ACF

Time Complexity

Time Complexity is O(XLen x YLen).

More topics